Rugby ball

This example follows the classic "rugby ball" example by Borrvall & Petersson 2003.

The objective is to minimize the dissipation

\[ \mathcal{F} = \frac{1}{|\Omega_\text{obj}|}\int \frac{1}{2} \left[ \nabla \mathbf{u} \cdot \left(\nabla \mathbf{u} + (\nabla \mathbf{u})^T \right) + \chi \mathbf{u} \cdot \mathbf{u} \right] d\Omega, \]

subject to a volume constraint

\[ \mathcal{C} = \frac{1}{|\Omega_\text{opt}|}\int_{\Omega_\text{opt}} \rho d\Omega. \]

More information regarding objectives and constraints can be found in Objectives and constraints.

The following depicts the optimization history for various volume constraints

Design field.

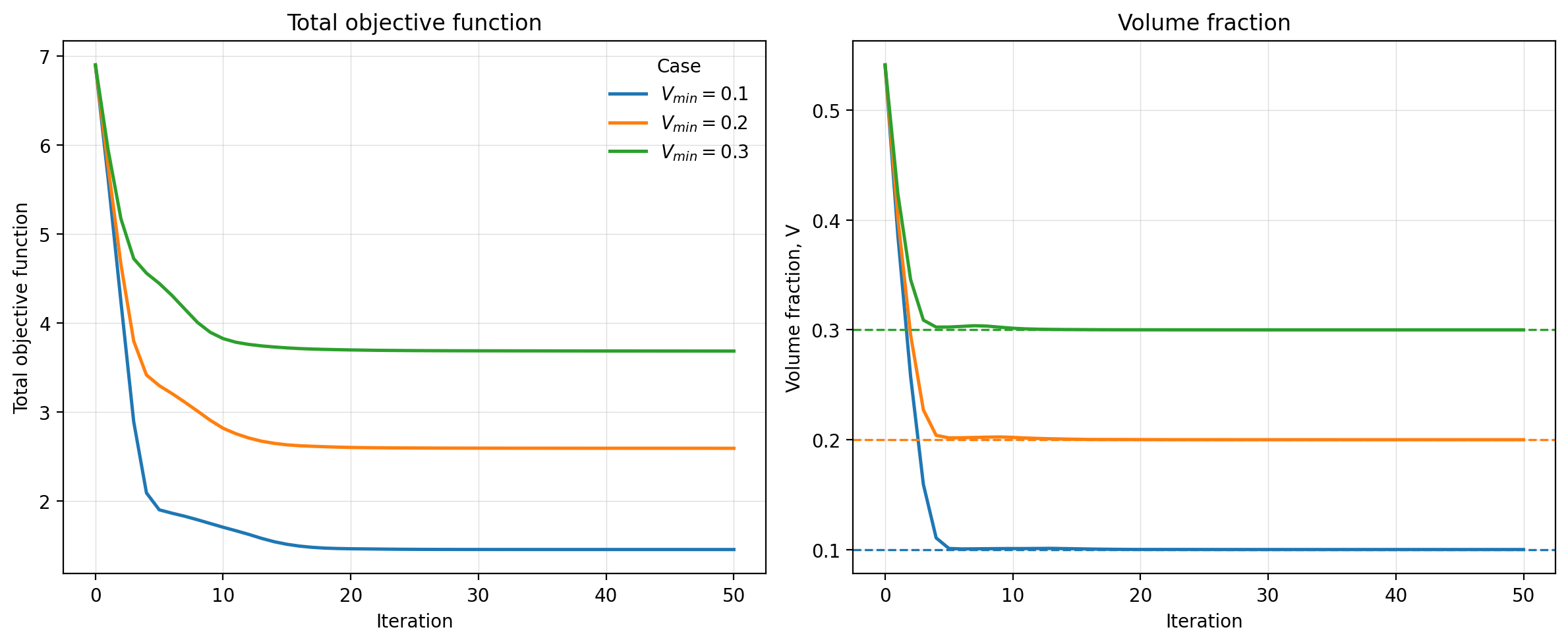
Convergence history.